Threshold Signature Scheme

Original presentation by Jinwoo Lee on Nov 7, 2024

1. Elliptic Curve over Finite Field

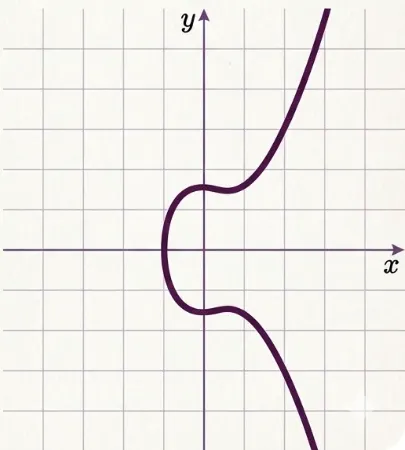
1.1. secp256k1 Elliptic Curve

Finite Field (유한체)

유한체 위에 있으므로 유한체를 정의하기 위한 prime number $p$가 필요합니다.

1.2. Cyclic Group (순환군)

정의

• 군 $G$가 하나의 원소 $g$로부터 생성될 수 있을 때 순환군이라고 합니다. $G = \langle g \rangle = \{g^n \mid n \in \mathbb{Z}\}$
• $g$: Generator(생성원)
• 순환군이면 아벨군(가환군)입니다. (교환법칙 성립)

Group (군)의 성질:

1. 닫혀있음 (Closure): 연산 결과가 항상 군 안에 존재.
2. 결합 법칙 (Associativity): $(a+b)+c = a+(b+c)$.
3. 항등원 (Identity): $a+0 = a$.
4. 역원 (Invertibility): $a+(-a) = 0$.

Order (위수)

하나의 Base Point로 시작해서 + 연산을 계속하다 보면 다시 처음의 Base Point로 돌아오게 됩니다. 이때 처음으로 돌아오는 연산 횟수 $n$을 순환군의 Order(위수)라고 부릅니다.

왜 순환군인가? 유한체에 대한 타원곡선 위의 임의의 점을 Base Point $G$로 잡고 연산을 정의하면 순환군을 이룹니다. 이때 순환군의 위수 $n$은 $p$와 다를 수 있습니다.

타원곡선 연산 시 주의할 점

• 점 연산 (타원곡선 방정식): $\text{mod } p$ 사용
• 스칼라 연산 (점 앞에 붙는 계수): 위수를 사용하여 $\text{mod } n$ 사용

1.3. 무한원점 & 타원곡선 덧셈 연산

Base Point $G$ $\rightarrow$ 타원곡선 위의 점 $(x_g, y_g)$에 대해 Private Key $x$만큼 덧셈 연산을 하여 Public Key를 얻을 수 있습니다.

• $P$: Public Key
• $x$: Secret Key
• $G$: Base Point

Base Point에 대해 $x$만큼 덧셈을 하는 것은 쉽지만, $P, G$로부터 $x$를 알아내는 것은 수학적으로 매우 어렵다고 알려져 있습니다 (Discrete Logarithm Problem).

• Uncompressed Pubkey: $P_x$ (32bytes) + $P_y$ (32bytes) + prefix 0x04 = 65bytes
• Compressed Pubkey: $P_x$ (32bytes) + prefix 0x02/0x03 ($y$ 부호) = 33bytes
• Secret Key: 32bytes

2. Digital Signature using Elliptic Curves

2.1. Create Signature

Given Key Pair: $P$ (Public), $x$ (Secret) where $1 < x < n$.

1. Random Nonce $k$ 생성: $1 < k < n$

2. Point $R$ 계산: $R = kG, \quad r = R_x$

3. Signature $(r, s)$ 생성: $s = k^{-1}(m + rx) \pmod n$ ($m$: message hash, $k^{-1}$: inverse of $k$)

2.2. Verify Signature

$s$에 대한 수식을 변형하여 검증합니다.

양변에 $G$를 곱하고 $R=kG, P=xG$를 대입합니다:

1. 좌변 $R$은 서명 $(r,s)$의 $r$로부터 얻을 수 있습니다.
2. 우변은 $m, s, r, P, G$를 대입하여 계산합니다.
3. 좌우변의 $x$좌표가 같음을 보이면 검증 완료입니다.

Note: secp256k1은 recovery 메서드를 지원하여, 서명과 메시지만으로 Public Key를 복구할 수 있습니다. 이를 위해 서명에 v 값을 포함합니다.

3. TSS (Threshold Signature Scheme)

• SSS (Shamir Secret Sharing): 비밀키를 나눠 갖고, $k$개를 모아 복구하여 사용합니다.

  • 단점: 복구 시점에 Single Point of Failure가 발생합니다.

• TSS: 키를 나눠 가진 상태에서, 비밀키 복구 없이 각자 부분 서명(Partial Signature)을 생성하고, 이를 합쳐 완성된 서명을 만듭니다.

3.1. Schnorr Signature

Create & Verify

1. 난수 $k$ 및 $R$ 값 계산: $R = kG$
2. Challenge $c$ 계산: $c = H(R \parallel M)$
3. 서명 $s$ 계산: $s_{schnorr} = (k + cx) \pmod n$

서명 결과: $(R, s)$

Verification

좌변($sG$)과 우변($R + cP$)이 같음을 확인합니다.

Advantage

• Linearity: Multi-Signature와 Aggregation에 유리합니다.
• Zero Knowledge Proof: 비밀키 $x$를 노출하지 않고 소유를 증명할 수 있습니다.

3.2. Cryptographic Architecture of TSS

과정을 3단계로 나누어 살펴봅시다.

1) Sharing Secret and Nonce

1. Secret Key Sharing: MPC 참여자가 비밀키 $x$를 SSS로 나눠가집니다.

   $$x = \sum_i x_i \lambda_i, \quad P_i = x_iG$$

2. Nonce Sharing: Nonce $k$는 나누는 것이 아니라, 각자 난수 $k_i$를 생성한 후 합치는 방식입니다.

   $$k = \sum_i k_i \lambda_i$$

2) Create Partial Signature ($r_i, s_i$)

각 참여자는 자신의 파편으로 부분 서명을 생성합니다.

3) Aggregate Partial Signatures

부분 서명들을 합쳐(Interpolation) 하나의 서명을 만듭니다.

4) Verify Complete Signature

외부에서는 이것이 단일 서명인지, MPC 서명인지 구분할 수 없습니다.

4. Code Example

mpc-cmp Schnorr ZK Proof implementation (pseudo-C code):

#include "crypto/zero_knowledge_proof/schnorr.h"

// 슈노르 ZK Proof 생성
static zero_knowledge_proof_status schnorr_zkp_generate_impl(...)
{
    // 1. R = kG
    status = algebra->generator_mul(algebra, &proof->R, &k);

    // 2. Challenge c = H(prover_id || R || public_data)
    SHA256_Init(&sha_ctx);
    SHA256_Update(&sha_ctx, prover_id, id_len);
    SHA256_Update(&sha_ctx, proof->R, sizeof(proof->R));
    SHA256_Update(&sha_ctx, *public_data, sizeof(elliptic_curve256_point_t));
    SHA256_Final(c, &sha_ctx);

    // 3. s = k - c * x
    status = algebra->mul_scalars(algebra, &c, secret, secret_size, c, sizeof(c));
    status = algebra->sub_scalars(algebra, &proof->s, k, sizeof(k), c, sizeof(c));

    return ZKP_SUCCESS;
}